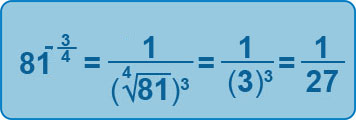Laws of indices
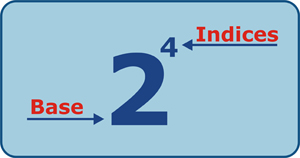
Indices are the small numbers in the top right corner of a number and raise your base to a power, e.g. 24 = 16 because it means 2x2x2x2.
You should be familiar with the powers and roots of number up to 152 and 53.
When dealing with indices, there are some shortcuts that you should be familiar with when making calculations and these are used not only for numbers, but also when dealing with letters. However, the shortcuts will only work if you have the same base!
Multiplying Indices
23 x 24 can be broken down as follows:
Similarly, 510 x 53 is simplified to 513.
(Check: 9 765 625 x 125 = 1 220 703 125 and 513 = 1 220 703 125)
However if we have 34 x 42 this cannot be simplified as the bases are both different.
We can test this by looking at common mistakes made:

When we check the answer with the calculator, 34 = 81 and 42 = 16, therefore the final answer is in fact 1 296.
Therefore, the general algebraic form of simplifying indices when multiplying is:
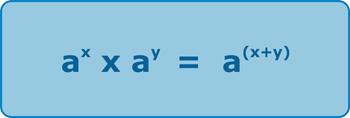
Notice that the base – a – is the same in both parts of the calculation.
Dividing Indices
28 ÷ 23 can be broken down as follows:
Similarly, 510÷ 53 is simplified to 57.
(Check: 9 765 625 ÷ 125 = 78 125 and 57 = 78 125)
However if we have 34÷ 42 this cannot be simplified as, once again, the bases are both different.
34 = 81 and 42 = 16 and when these two values are divided, the result (5.0625) cannot be simplified into index form.
Therefore, the general algebraic form of simplifying indices when dividing is:
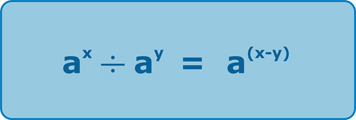
Notice once again, that the base – a – is the same in both parts of the calculation!
Raising a power to a power
When we have to deal with something like:
(53) 2, then we simply multiply the powers, as this becomes 5(3x2) = 56. This makes sense, because what this calculation actually means, is 53 all squared and using our rule for multiplying indices, we can simplify as follows:
53 x 53 = 56
Hence, the general rule is:
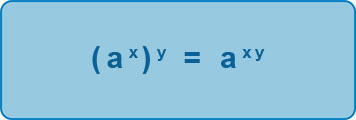
Negative Indices
When an index is negative, this means that the base is raised to the power of the number given BUT it is a reciprocal, i.e. basically, we put ‘1 over’ the number.
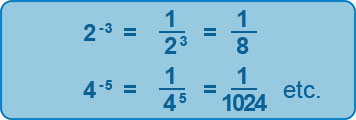
Indices as roots
Raising a number to any power is quite straightforward, but when you have the inverse, we are looking at raising a power to a root. This is known as finding the nth root of a number, a, and can be written as:
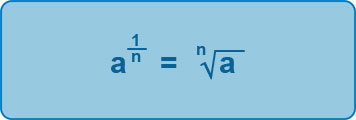
This is where you will see how important it is to remember your roots as much as possible!
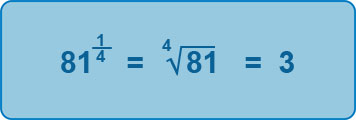
Harder Fractional Powers
However, inevitably, there are trickier roots you need to be able to find and this is where we start delving into the realms of AS Level Maths! The above example just considers the numerator in the fraction being 1, but we need to consider a generalisation when the numerator is an integer > 1:
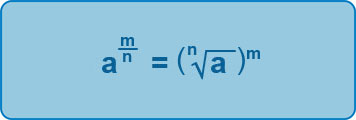
Therefore, if we have:
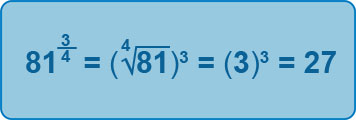
As can be seen, we need to find the nth root first, and then raise this answer to the power indicated by the numerator in the fraction.
If we have negatives, as well as the fractions, the result will be that the result will be a reciprocal.
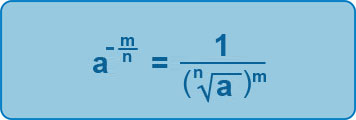
So: