Momentum

Momentum is defined as the product of mass and velocity.

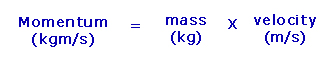
The unit for momentum is kilogram meters per second (kgm/s) and it is a vector quantity as it has both size and direction. The direction is given by the velocity (velocity = speed in a particular direction).

Momentum has the symbol “p” and can be written mathematically as:

p = m x v

 

Thus, the momentum of an object depends on its mass and its velocity. A 5000kg van travelling with a velocity of 6m/s will have a greater momentum than a 2000kg car travelling at the same velocity of 6m/s. However, a 2000kg car travelling at a velocity of 20m/s will have a greater momentum than the 5000kg van travelling at 6m/s.

From Newton’s second laws we know that:

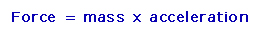
And that the acceleration is the change in velocity by the time taken:

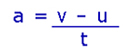
By substituting the value of “a” into the force equation it gives:

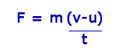
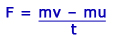
The above equation can be written as:

Resultant Force x time taken = change in momentum

This equation confirms that when a resultant force acts on an object it will cause a change of momentum in the direction of the force and the size of the change depends on the size of the force and the time for which it acts.

This can be explained by considering a sportsman or sportswoman striking a ball. A good sportsperson will always follow through when playing a shot.  This means the force is applied for a longer time and so a greater change in momentum can be achieved for a given force.

 

 

Let’s consider the following example. A batsman strikes a cricket ball of mass 0.15kg accelerating it from 10m/s to 25m/s. The illustration below shows the force required when the bat acts on the ball for 1/100th of a second and for 1/10th of a second.

The above example illustrates that the longer the duration of contact or impact in a collision the smaller the force exerted. Seat belts, airbags and crumple zones in cars also make use of this concept. During a car accident the seat belt is designed to stretch slightly, thereby increasing its time of contact with the wearer. This reduces the force of the impact on the seat belt wearer. Crumple zones in vehicles also increase the length of time of impact with a colliding object thus reducing the force on the passengers.

 

Conservation Of Momentum

We know from the equation mentioned in the section above that when a force acts on a body for a time it results in a change of momentum. When two bodies collide they exert a force over the same period of time which results in a change in momentum. From Newton’s third law we know if object A exerts a force on object B then object B exerts an equal and opposite force on object A.
This means that the change in momentum will be equal and opposite.

The principle of conservation of momentum is as follows:

Total momentum before collision = total momentum after collision

For the principle of conservation to hold no external forces must act on the colliding bodies as this would result in momentum being added to the system.

The principle of conservation of momentum also applies to explosions. Explosions are the opposite to collisions. In explosions objects move apart. An example of this is a rocket. A rocket gains momentum by the controlled explosion of fuel as the hot exhaust gases move in one direction the rocket moves in the opposite direction. Thus the momentum of the hot exhaust gases equals the momentum of the rocket.

---