The Expanding Universe
All the galaxies we can view are moving away from us. This observation was first made by Edwin Hubble in 1929. Hubble did this by analysing the light from the brightest stars in different galaxies. Knowing that the light from stars is produced by the burning of known elements he could compare the spectrums.
Each chemical element has a distinct spectrum or in other words each element produces a specific array of coloured lines. These spectrums are produced by burning the element and dispersing the light given off to form a spectrum. Scientists have produced spectra for all the different elements. Therefore, in order to learn the composition of a star they photograph it and compare its spectrum with the spectra of the known elements. By obtaining an exact match they can determine the elements which make up the star.
This is the approach Edwin Hubble took. By comparing the spectrums from giant stars in different galaxies he noticed a difference in the spectra from stars of distant galaxies to the ones closer to Earth. Considering the light from giant stars is from burning the same elements the difference in the spectrum must be due to relative motion of the source. For the distant galaxies he noticed that the lines were shifted away from their normal wavelengths towards the red, long wavelength part of the spectrum. This phenomenon is referred to as red shift and to understand this, the Doppler Effect first needs to be explained.
The Doppler Effect
The Doppler Effect is a phenomenon in which the observed frequency of a source is less or more than the true frequency as a result of either the source or the observer or both moving. It takes it name from Christian Doppler who came up with this idea in 1842.
The animation below explains the Doppler Effect using sound waves.
Doppler Effect using Sound Waves
When the police car is still and the siren is sounding the sound is coming from a stationary source. The sound waves travel equally in all directions.
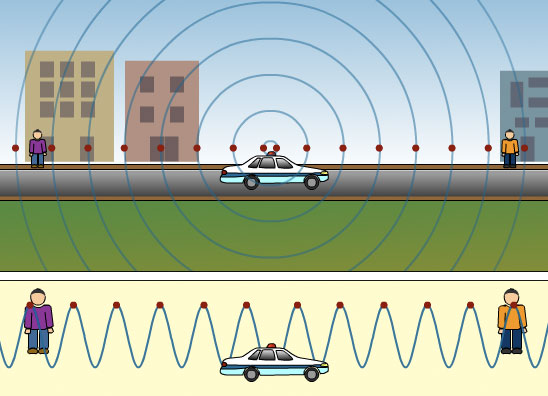
The velocity of sound in air is approximately 330 meters per second (depending on air temperature). The wavelength and the frequency of the sound waves from the police car is the same in all directions. Therefore, observers on any side of the police car would hear the exact same sound.
Remember the wave equation,
| Velocity of a wave | = | frequency | x | wavelength |
| v | f | λ | ||
| meters per second | per second | meters |
We know the speed of sound in air is 330m/s and the wavelength for the sound waves from the siren are 1m. Therefore, the frequency can be calculated as:
Frequency (f) = velocity/wavelength
Frequency (f) = 330/1 = 330 seconds-1 or 330 Hertz
As the police car moves forward it catches up with part of the sound waves in front of it. The waves in the front become bunched up and have a shorter wavelength. Therefore there is an apparent change in the frequency of the waves at the front of the car. Wavelength and frequency are related, so the shorter wavelengths give a higher frequency which in turn gives a high pitch.
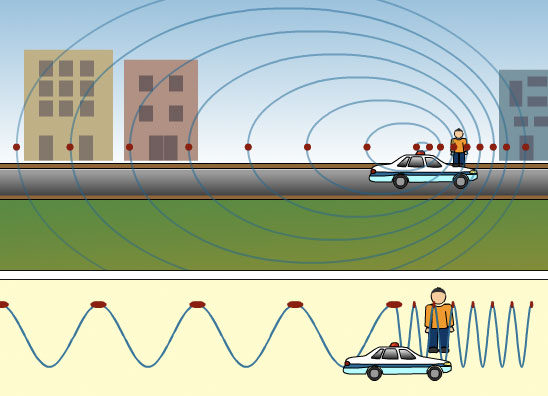
Remember the wave equation as this gives the relationship between wavelength an frequency:
| Velocity of a wave | = | frequency | x | wavelength |
| v | f | λ | ||
| meters per second | per second | meters |

The speed of sound in air remains the same so is 330m/s and the wavelength for the sound waves from the siren in front of the car has halved to 0.5m. Therefore, the frequency can be calculated as:
Frequency (f) = velocity/wavelength
Frequency (f) = 330/0.5 = 660 seconds-1 or 660 Hertz
Halving the Wavelength doubles the Frequency
HIGH FREQUENCY = HIGH PITCH
After the car passes by the person, the waves behind the car are stretched out and have a longer wavelength. Therefore there is also an apparent change in the frequency of the waves behind the car. Wavelength and frequency are related, so the longer wavelengths give a lower frequency which in turn gives a low pitch.
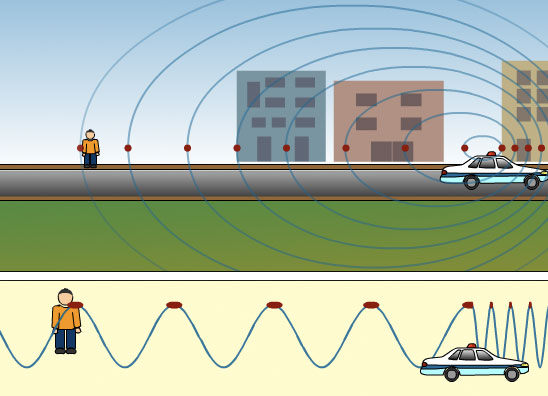
Remember the wave equation as this gives the relationship between wavelength an frequency:
| Velocity of a wave | = | frequency | x | wavelength |
| v | f | λ | ||
| meters per second | per second | meters |
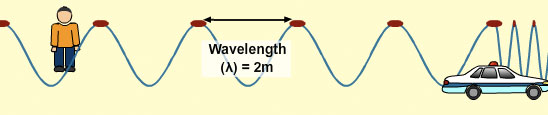
The speed of sound in air remains the same so is 330m/s and the wavelength for the sound waves from the siren in front of the car has doubled to 2m. Therefore, the frequency can be calculated as:
Frequency (f) = velocity/wavelength
Frequency (f) = 330/2 = 165 seconds-1 or 165 Hertz
Doubling the Wavelength halves the Frequency
LOW FREQUENCY = LOW PITCH
