The Four Operations for Fractions
Adding and Subtracting Fractions
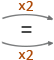
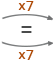
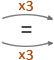
You must NEVER add/subtract unless the denominator is the same for each fraction (if they aren’t the same, you need to find equivalent fractions) and more importantly, NEVER add/subtract the denominators!
Following these steps should help:
Step 1: Make sure the denominators are the same, if not change them.
Step 2: Add/subtract the numerators and put the answer over the denominator.
Step 3: Simplify the final answer.
Examples
Example 1 |
| What is 310 + 110 ? |
Solution:
Notice the answer is NOT 220 and the final answer has been simplified to 25 as both the numerator and denominator have been divided by 2. |
Example 2 |
| What is 78 − 34 ? |
Solution: Make denominators the same:
Now subtract,
|
Adding and Subtracting Mixed Fractions
Step 1: Convert mixed fractions to improper fractions.
Step 2: Make sure the denominators are the same, if not change them.
Step 3: Add/subtract the numerators and put the answer over the denominator.
Step 4: Simplify the final answer/convert back to mixed fraction.
Example 3 |
| What is 4 25 − 2 37 ? |
Solution: Convert to improper fractions:
To find a common denominator we find the Lowest Comon Multiple (LCM) of 5 and 7, which is 35. So,
Now subtract,
Convert back to mixed fraction:
|
Example 4 |
| What is 1 56 − 2 34 ? |
Solution: Convert to improper fractions:
To find a common denominator we find the Lowest Comon Multiple (LCM) of 6 and 4, which is 12. So,
Add:
Convert back to mixed fraction:
|