The Four Operations for Fractions

Multiplying Fractions

This is much easier than adding and subtracting, as you don’t have to remember to make the denominators equivalent, but you can only multiply if the fractions are TOP HEAVY. Once you have changed any mixed numbers you have, you simply multiply the numbers across the numerators and denominators and don’t forget to simplify at the end.

Examples
1.	3 x 4 = 12 5 7 35
2.	4 1 x 2 3 2 11	(you MUST change to improper fractions)
	= 9 x 25 2 11	(now multiply the numbers across)
	= 225   =   10 5 22 22

 

From the second example, you should notice that things can get tricky when the numbers you are multiplying are too big. This is where you should look for cancelling/simplifying your fractions as much as possible, before multiplying the numbers. This is particularly important to do when you are in a non-calculator exam as you don’t want to be tied up trying to multiply and hence cancel very large numbers.

 

---

 

3.	6 3 x 2 2 10 9
	= 63 x 20 10 9	ANY numerator can be cancelled with ANY denominator
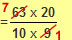		both ‘9’ and ‘63’ can be divided by 9!
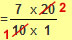		both ‘10’ and ‘20’ can be divided by 10!
	= 7 x 2 1 x 1
	= 14
4.	3 3 x 1 13 7 36
	= 24 x 49 7 36
		both ‘24’ and ‘36’ can be divided by 12, but you can start with 6.
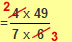		both ‘4’ and ‘6’ can now be divided by 2, to complete simplifying.
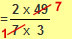		both ‘7’ and ‘49’ can be divided by 7.
	= 2 x 7 1 x 3
	= 14 3
	= 4 2 3

 

---